Umfang und Flächeninhalt von Rechtecken
Unterrichtsideen zum Thema: Umfang und Flächeninhalt von Rechtecken
Die Berechnung von Umfang oder Flächeninhalt findet oft zu früh anhand von Formeln auf einer abstrakten Ebene statt. Auf diese sollte man sich erst begeben, wenn entsprechende Grundvorstellungen sicher verankert sind. Diese werden in der Regel schrittweise unter Berücksichtigung des EIS-Prinzips entwickelt:
- Enaktiv: Aktiv handelnd mit konkretem Material
- Ikonisch: Im Umgang mit Bildern und Skizzen
- Symbolisch: Auf der abstrakten Ebene z.B. im Umgang mit Formeln oder (Fach)sprache
Beispiel für das Arbeiten auf der enaktiven Ebene mit konkreten Materialien:
- Mit Messgeräten (Lineal, Meterstab, Maßband) die Umgebung erkunden
- Flächen aus Blumendraht biegen
- Mit Papierstreifen Flächen „einzäunen“
- Mit Streichhölzern Flächen legen
- Mit Einheitsquadraten Flächen legen
- Flächen auf dem Nagelbrett aufspannen
- Arbeiten mit Karten und Stadtplänen
- ………
Mit der Navigation in der rechten Randspalte gelangen Sie auf Seiten, auf denen einige der obigen Beispiele näher erläutert werden.
Eine Zusammenfassung der Inhalte dieser Seiten steht Ihnen auch als Word - Dokument zur Verfügung
Interaktive Online-Übung mit einer GeoGebra-Animation
Unter dem nachfolgenden Link gelangen Sie zu einer Online-Übung, bei der sowohl der Flächeninhalt als auch der Umfang von Rechtecken berechnet werden muss. Mit Hilfe der Animation werden die Rechnungen augenblicklich korrigiert und bei Erfolg mit Punkten belohnt.
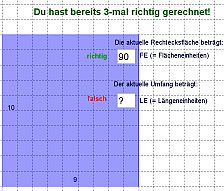
Die Übung eignet sich sehr gut als Kopfrechentraining. Da hier darüber hinaus spielerisch auf die Reihen- bzw. Spaltenanordnung von Einheitsquadraten bei Rechtecken eingegangen werden kann, eignet sich die Animation zusätzlich als Vorübung für die Umrechnungsfaktoren bei Umformungen die nächstgrößere bzw. nächstkleinere Flächeneinheit, .
Interaktive GeoGebra-Übung zum Umfang und Flächeninhalt beim Rechteck
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.



