Bernoulli-Ketten und Binomialverteilung
Bei einem Bernoulli-Experiment gibt es genau zwei verschiedene Ausgänge. (Meist spricht man von Treffer/kein Treffer oder Treffer/Niete.) Mit der Angabe der so genannten Trefferwahrscheinlichkeit p lässt sich dadurch die Wahrscheinlichkeit für kein Treffer durch 1-p sofort bestimmen. Diese Wahrscheinlichkeit wird allgemein mit q abgekürzt.
Beispiel:
Beim Würfeln interessiert nur, ob eine 6 gewürfelt wird. Die Trefferwahrscheinlichkteit beträgt hierbei p=1/6, die Wahrscheinlichkeit für Niete dementsprechend q=1-1/6=5/6.
Bernoulli-Ketten und deren Darstellung im Baumdigramm
Bei der wiederholten Ausführung eines Bernoulli-Experiments kann man auch von einer Bernoulli-Kette sprechen, wenn die Trefferwahrscheinlichkeit bei den einzelnen Teilexperimenten gleich bleibt. Wird bei einer Bernoulli-Kette das Bernoulli-Experiment n mal wiederholt, spricht man von einer Bernoulli-Kette der Länge n.
Beispiel:
Es darf drei Mal gewürfelt werden. Die Zahl der hierbei gewürfelten Sechsen wird notiert.
Bei einer Bernoulli-Kette wird bei jedem Schritt über Treffer und Niete entschieden. Nach k Schritten kann somit die (Gesamt-)Trefferzahl zwischen 0 und k liegen. Dies lässt sich in einem Baumdiagramm veranschauen. Hierbei ist zu beachten, dass es in der Regel mehrere günstige Pfade gibt. Diese günstigen Pfade sind in der nachfolgenden Animation grün markiert. Mit den Schiebereglern lassen sich in der Animation die Trefferzahl und die Länge der Bernoulli-Kette verändern.
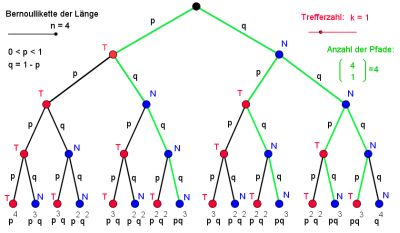
Baumdiagramme zu Bernoulli-Ketten bis zur Länge von n=4
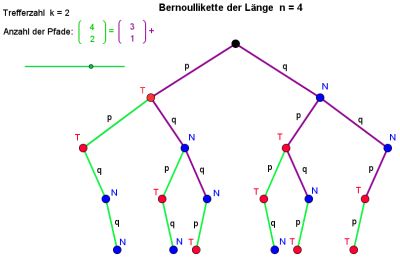
Rekursionsformel für Binomialkoeffizienten
Die Binomialkoeffizienten lassen sich kinderleicht mit dem Pascalschen Dreieck bestimmen. Die Rekursionsformel, die dem Pascalschen Dreieck zu Grunde liegt, lässt sich mit der nachfolgenden Animation anschaulich belegen. Schieben hierzu den Schieberegler schrittweise nach rechts und begründen Sie die Veränderungen der Formel mit den farblichen Veränderungen im Baumdiagramm.
Beispielaufgabe mit Wahrscheinlichkeit P(X=k) und Formel von Bernoulli
Am Beispiel eines Multiple-Choice-Tests werden im folgenden Dokument Wahrscheinlichkeiten für verschiedene Trefferanzahlen berechnet. Eine Verallgemeinerung führt auf die Bernoulli-Formel 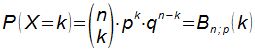
Dokument-Download als PDF-Datei:
Histogramm / Balkendiagramm als Darstellungform einer Wahrscheinlichkeitsverteilung
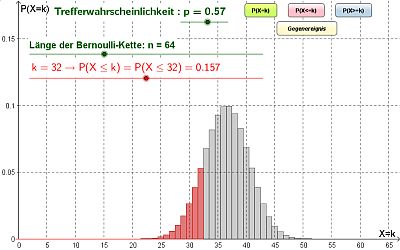
Mit Histogrammen lassen sich Wahrscheinlichkeitsverteilungen bei Bernoulli-Ketten anschaulich darstellen. Daher kann die nachfolgende Animation zur Erklärung von Taschenrechner-Ergebnissen oder Werten aus Wahrscheinlichkeitstabellen als Verständnishilfe dienen.
Das Histogramm unterstützt Sie bei binomialverteilten Zufallsvariablen (Bernoulli-Ketten) bis zu einem Umfang von n=200.
Histogramm zu binomialverteilten Zufallsvariablen
Binomialverteilung und Erwartungswert bei binomialverteilten Zufallsvariablen
Mit Hilfe der obigen Bernoulli-Formel erhält man für jede mögliche Trefferzahl k einen Wahrscheinlichkeitswert P(X=k). Im zugehörigen Wahrscheinlichkeits-Histogramm wird jede dieser Wahrscheinlichkeiten durch einen Balken dargestellt.
Bei der hier vorgestellten Animation lassen sich die Länge der Bernoulli-Kette und die Trefferwahrscheinlichkeit mit Hilfe von Schiebereglern verändern. Automatisch ergibt sich hier eine Vermutung über den Zusammenhang von Erwartungswert und dem Maximum der Wahrscheinlichkeitsverteilung.
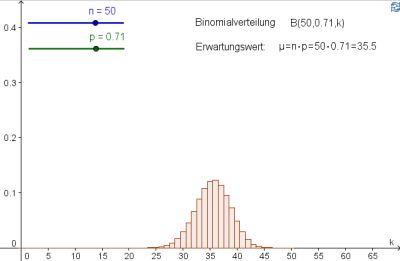
Binomialverteilung und Erwartungswert bei binomialverteilten Zufallsvariablen
Beispielaufgabe mit Erwartungswert einer binomialverteilten Zufallsvariablen
Am Beispiel von Basketball-Freiwürfen wird der Erwartungswert berechnet.
Dokument-Download als PDF-Datei:




