Proportionale und lineare Funktionen in der Realschule
Die folgenden Materialen zur Leitidee "Funktionaler Zusammenhang" sollen Schülerinnen und Schülern der 8. Klasse dabei helfen, dass sie
- eine Gerade mit der Gleichung y = mx + b unter Verwendung von Steigung und Steigungsdreiecken zeichnen
- und einer Geraden eine Gleichung zuordnen können.
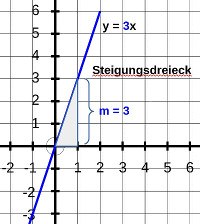
1. Das Schaubild der proportionalen Funktion y = mx
Erklärvideo: Wie zeichne ich den Graphen der Funktion y = 3x ?
|
|
Wertetabelle
| x | -2 | -1 | 0 | 1 | 2 |
| y | -6 | -3 | 0 | 3 | 6 |
Setzt man für x unterschiedliche Zahlenwerte in die Funktionsgleichung ein, erhält man die dazugehöigen y - Werte.
Diese Zahlenpaare (x;y) kann man übersichtlich in einer Wertetabelle darstellen und als Punkte in ein Koordinatensystem einzeichnen.
Diese Punkte liegen alle auf der Geraden mit der Funktionsgleichung y = 3x
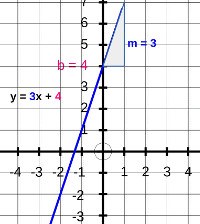
2. Der Graph der linearen Funktion y = mx + b
Erklärvideo: Wie zeichne ich den Graphen der Funktion y = 3x +4 ?
|
|
Wertetabelle
| x | -2 | -1 | 0 | 1 | 2 |
| y | -2 | 1 | 4 | 7 | 10 |
Setzt man für x unterschiedliche Zahlenwerte in die Funktionsgleichung ein, erhält man die dazugehöigen y - Werte.
Diese Zahlenpaare (x;y) kann man übersichtlich in einer Wertetabelle darstellen und als Punkte in ein Koordinatensystem einzeichnen.
Diese Punkte liegen alle auf der Geraden mit der Funktionsgleichung y = 3x + 4
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.