Wahrscheinlichkeiten bestimmen
Du kannst Wahrscheinlichkeiten zu einem Zufallsexperiment entweder mit Symmetrieüberlegungen bestimmen (z. B. Münzwurf, Glücksrad, Würfel) oder nach vielen Wiederholungen des Zufallsexperiemtes durch Berechnung der relativen Häufigkeiten der günstigen Ergebnisse (z. B. Reißnagelwurf). Bei der zweiten Vorgehensweise erhältst du verständlicherweise nur einen Näherungswert (s. u.)
Fall 1: Bestimmung der Wahrscheinlichkeiten bei Laplace-Experimenten
Beim Wurf mit einem Würfel ist die jedes Elementarereigis gleich wahrscheinlich. Zufallsexperimente mit dieser Eigenschaft nennen wir Laplace-Experimente.
Die Wahrscheinlichkeit für ein Ereignis A bei Laplace-Experimenten ist daher gleich dem Verhältnis der Anzahl der Ergebnisse, bei denen das Ereignis A eintritt, zur Gesamtzahl aller möglichen Ergebnisse des Zufallsexperiments:
![]()
Beispiele:
- Beim Roulette gibt es 37 mögliche Ergebnis (die Zahlen von 0 bis 36). Bei einem Einsatz "impair" (ungerade Zahl) gibt es 18 Gewinnmöglichkeiten. Damit beträgt die Gewinnwahrscheinlichkeit 18/37.
- Beim zweimaligen Würfeln gibt insgesamt 36 verschiedene Augenkombinationen. Von diesen 36 Kombinationen liefern genau sechs die Augensumme 7. Daher ist die Wahrscheinlichkeit für die Augensumme 7 bei zwei Würfen gleich 6/36 = 1/6.
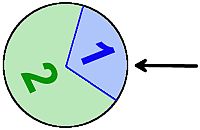
- Bei einem Glücksrad ist die Anzeige für jeden gleich großen Sektor gleich wahrscheinlich. ("Sektor" ist der Fachbegriff für ein "Kuchenstück").
Beim nebenstehende Glücksrad ist ein Drittel der Fläche blau, daher kannst du die Wahrscheinlichkeit für blau mit einem Drittel angeben.
Fall 2: Bestimmung von Wahrscheinlichkeiten aus relativen Häufigkeiten
Etwas mühsamer ist die Bestimmung von Wahrscheinlichkeiten, wenn die Symmetrie nicht oder nur schwer berechenbar ist. Gehe in diesem Fall am besten in zwei Schritten vor:
- Führe das Zufallsexperiment ganz oft durch. Merke dir die Zahl der Durchführungen und dokumentiere die einzelnen Ergebnisse (z. B. mit einer Strichliste). Am Ende erhältst du zu jedem Ergebnis eine Zahl - die so genannte absolute Häufigkeit.
- Teile im zweiten Schritt die absolute Häufigkeit durch die Gesamtzahl der Durchführungen. Dieses Verhältnis ist die so genannte relative Häufigkeit. Je mehr Durchführungen du gemacht hast, umso besser nähern die relativen Häufigkeiten die tatsächliche Wahrscheinlichkeit für das Eintreffen eines Ereignisses an.
Grundlage dieser Vorgehensweise ist das empirische Gesetz der großen Zahlen. Es besagt, dass sich bei einem Zufallsexperiment die relativen Häufigkeiten bei einer großen Zahl von Durchführungen nicht mehr wesentlich verändern. Sie nähern sich dabei umso besser an den theoretischen Wert der Wahrscheinlichkeit an, je öfter das Zufallsexperiment durchgeführt wird. Eine schöne Animation zum empirischen Gesetz der großen Zahlen von Andreas Lindner verdeutlicht das Prinzip am Beispiel der Wahrscheinlichkeiten beim Würfel.
Beispiele:
- Bei einem Reißnagelwurf auf einer ebenen Unterlage werden bei sehr vielen Durchführungen ca. 60% aller Würfe auf dem Kopf landen, 40% der Versuche landen auf der Seite. Bei einer kurzen Versuchsreihe liegen die errechneten relativen Häufigkeiten oftmals deutlich über oder unter diesen Werten. (Je nach Form des Reißnagels können die oben angegebenen Werte natürlich auch variieren).
- Die Buchstabenhäufigkeit gibt an, wie häufig ein bestimmter Buchstabe durchschnittlich in einem Text einer Sprache vorkommt. Beispielsweise liegt der Anteil des Buchstaben e in einem deutschen Text bei ca. 17,4% von allen vorhandenen Buchstaben. In der englischen Sprache sind es nur 12,7% und im Polnischen sogar nur 6,9%.
Mit den Online-Programmen der nachfolgenden Links kannst du Texte mit copy & paste einfügen und die zugehörigen Häufigkeitstabelle erstellen: - Näherungswert für die Zahl pi:
Der Einheitskreis (Kreis mit Radius 1) hat laut Definition die Fläche pi.
Stell dir vor, du umschließt den Einheitskreis mit einem Quadrat der Seitenlänge 2. Anschließend schießt du rein zufällig ohne zu zielen auf das Quadrat. Jeder Punkt im Quadrat wird hierbei mit der gleichen Wahrscheinlichkeit getroffen.
Da die Fläche des Kreises pi beträgt und die des Quadrates 4, sollten die Trefferquote im Kreis ca. bei pi/4 liegen. Unter dem folgenden Link wird die Vorgehensweise mit einer Animation vorgeführt:


