Würfeln mit 2 Würfeln
1. Darstellungsmöglichkeiten der Ergebnismenge
Bei dem Zufallsexperiment Würfeln mit 2 Würfeln gibt es 36 mögliche Versuchsausgänge (Ergebnisse), also alle möglichen geordneten Paare von Augenzahlen.
a.) Mengenschreibweise
E = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3),... (6, 4), (6, 5) , (6, 6)}
b.) Grafische Darstellung
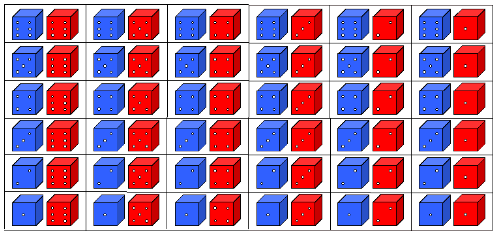
Tabellarische Darstellung der Augensummen
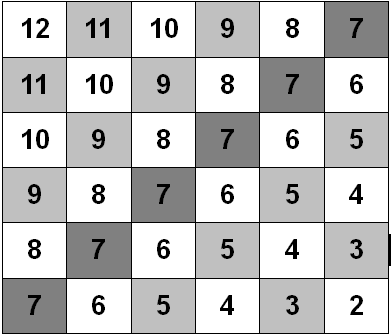
2. Ergebnisse mit zwei Würfeln
Ein Ereignis kann sich aus mehreren möglichen Ergebnissen zusammensetzen. Es ist eine Teilmenge der Ergebnismenge:
Bsp 1: Das Ereignis „gerade Zahl“ setzt sich aus 12 möglichen Ergebnissen zusammen
G = { (1,1) , (1,3) , (1,5) , (2,2) , (2,4) , (2,6) , (3,1) , (3,3) , (3,5) ,
(4,2) , (4,4) , (4,6) , (5,1) , (5,3) , (5,6) , (6,2) , (6,4) , (6,6) , }
Bsp 2: Das Ereignis „Augensumme 5“ setzt sich aus 4 möglichen Ergebnissen zusammen F = { (1,4) , (2,3) , (3,2) , (4,1) }
Bsp 3: Das Ereignis „Augensumme 8“ setzt sich aus 5 möglichen Ergebnissen zusammen A = { (2,6) , (3,5) , (4,4) , (5,3) , (6,2) }
3. Das sichere Ereignis – das unmögliche Ereignis – das Gegenereignis
- Das Ereignis „Augensumme 13“ ist ein Beispiel für ein unmögliches Ereignis. Die Ereignismenge ist die leere Menge E = { }
- Das Ereignis „Die Augensumme ist eine natürliche Zahl“ nennt man das sichere Ereignis, also alle möglichen Ergebnisse.
- Zu jedem Ereignis gibt es das Gegenereignis:
Ereignis„ Gerade Zahl“ Gegenereignis„„ungerade Zahl“
Ereignis„ „Augensumme 13“ Gegenereignis „Augensumme nicht 13“
Aufgaben:
Bestimme die Anzahl folgender Ereignisse beim Würfeln mit 2 Würfeln:
a.) Die Augensumme ist 1
b.) Die Augensumme ist 2
c.) Die Augensumme ist 10
d.) Beide Würfel zeigen die gleiche Zahl (Pasch)
4. Der Begriff Wahrscheinlichkeit „Laplace Formel“
Geht man davon aus, dass die Wahrscheinlichkeit für jedes Elementarergebnis gleich groß ist, so gilt in unserem Beispiel:
die Wahrscheinlichkeit für 1 von 36 möglichen Ergebnissen P(E) = 1/36 . Auf diese Weise erhalten wir eine Zahl, mit der wir die Wahrscheinlichkeit für das Eintreten eines Ereignisses bestimmen können.

Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.


