Das Newton-Verfahren
In der Differenzialrechnung spielt die Nullstellenbestimmung von Funktionen eine große Rolle. Denken wir dabei z. B. an die notwendigen Bedingungen für Extrem- und Wendestellen.
Mit einem grafikfähigen Taschenrechner (GTR) oder einem Computer-Algbra-System (CAS) ist diese Nullstellenbestimmung mittlerweile kein Problem mehr. Allerdings gab es noch vor 30 Jahren kaum leistungsfähige Taschenrechner. Hier war Kopfrechnen angesagt. Es stellt sich die Frage:
Wie finden wir Nullstellen ohne technische Hilfsmittel?
Im einfachsten Fall gelingt (evtl. durch Ausklammern) eine Produktdarstellung des Funktionsterms, so dass aus f(x)=0 der Typ Faktor 1 * Faktor 2 = 0 entsteht. Die Nullstellen können hierbei über die Nullstellen der Faktoren gefunden werden.
Bei quadratischen Funktionen gibt es für die Nullstellenfindung die Mitternachtsformel (bzw. p-q-Formel).
Leider gibt es auch Funktionen, für deren Nullstellenbestimmung uns kein Rechenwerkzeug zur Verfügung steht. Bei differenzierbaren Funktionen hilft uns eine kleine Formel von Isaak Newton, schrittweise zu einem Näherungswert für eine Nullstelle zu gelangen:
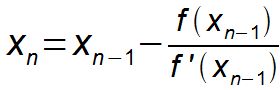
Im folgenden Dokument werden stichwortartig zwei Begründungen für diese Formel geliefert. Die erste Begründung benutzt die Tangentengleichung in der Punkt-Steigungsform, die andere die Definition der Geradensteigung am Steigungsdreieck.
Dokument als OpenOffice-Datei
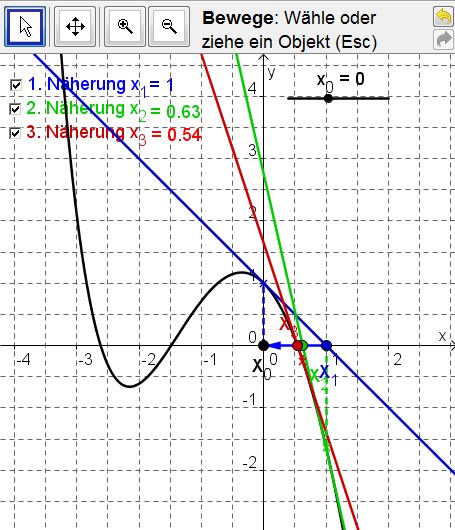
Eine Animation zum Newton-Verfahren
Die folgende Animation ermöglicht es, die ersten drei Näherungswerte für eine beliebige Funktion zusammen mit dem Schaubild und den entsprechenden Tangenten anzuzeigen. Bei der ersten Tangenten ist das Steigungsdreieck sichtbar, mit dem sich die obige Formel erklären lässt.
Für die Anzeige der Animation benötigen Sie Java. Daher kann der erste Aufruf etwas dauern. Zur Animation
