Vollständige Formulierung des Beweises

Beweis:

Teil 1: R teilt die Strecke 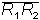R1,R2 genau in der Mitte

Die Voraussetzungen für unseren anfangs vorgestellten Satz sind erfüllt: da unsere beiden Streifen gleich breit sind, zerlegen sie die Strecke R1,R2 in zwei gleich große Stücke.
Somit gilt: 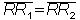R,R1=R,R2

Teil 2: Die "inneren roten Streckenstücke" sind gleich lang. Kurz: 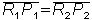R1,P1=R2,P2

Das (blaue) Dreieck MP2P1 ist gleichschenklig, da zwei Seiten Radien im Thaleskreis über M1, M2 (und daher gleich lang) sind.
Nun wird bei gleichschenkligen Dreiecken die Basis von der entsprechenden Höhe genau in der Mitte geteilt, d. h. es gilt R,P1=R,P2. Zieht man diese Strecken auf beiden Seiten der Gleichung von Teil 1 ab, folgt:
R1,P1=R2,P2

Teil 3: Die beiden roten Strecken (a und b) sind gleich

Auch in den beiden äußeren Kreise findet man gleichschenklige (rote) Dreiecke (M1P1Q1 und M2Q2P2) mit der gleichen Begründung wie im Teil 2 folgt hieraus die Gleichheit der "Basishälften". Die Strecken a und b sind somit genau doppelt so groß wie die Strecke R1,P1 (bzw. R2,P2).
Das war zu zeigen. q.e.d. (quod erat demonstrandum - was zu beweisen war)

Bemerkung:

Die Gleichheit der "Basishälften" in Teil 2 und 3 könnte man auch mit einer der folgenden Eigenschaften von gleichschenkligen Dreiecken begründen:
  • "Im gleichschenkligen Dreieck stimmen die Mittelsenkrechte, und die Seitenhalbierende der Basis überein." Da die Mittelsenkrechte senkrecht auf der Basis steht und die Seitenhalbierende durch den Basismittelpunkt und die gegenüberliegende Ecke geht, ist damit alles gezeigt.
  • "Die Mittelsenkrechte der Basis ist beim gleichschenkligen Dreieck Symmetrieachse." Durch eine Achsenspiegelung an der Mittelsenkrechten der Basis würde somit die eine "Basishälfte" auf die andere überführt.