Quadratzahlen

Quadratzahlen besitzen viele interessante Eigenschaften, mit deren Hilfe du anschaulich ein verbessertes Zahlenverständnis erlangen kannst. Zunächst betrachten wir die Definition:
Zahlen, die sich als Produkt zweier gleicher natürlicher Zahlen (ungleich null) darstellen lassen, heißen Quadratzahlen.
Die kleinste Quadratzahl ist 1, denn 1*1=1. Die nächste Quadratzahl ist 4, da 2*2=4. Weitere Beispiele für Quadratzahlen sind 9, 16, 25, …
Der Begriff Quadratzahl beschreibt die Tatsache, dass man diesen Zahlentyp mit Quadraten veranschaulichen kann. In der nebenstehenden Skizze wird die Zahl 36 durch sechs Reihen zu je sechs Kreuzen dargestellt.
Animation: Darstellung von Quadratzahlen (1² bis 11²)
Eigenschaften von Quadratzahlen (Mit Animationen)
 Der Abstand von einer Quadratzahl zur nächsten ist immer eine ungerade Zahl. Jede Quadratzahl lässt sich somit aus einer Summe von ungeraden Zahlen darstellen. Es ist sogar so, dass die Summe der ersten n ungeraden Zahlen genau die n-te Quadratzahl n² ergibt.
Der Abstand von einer Quadratzahl zur nächsten ist immer eine ungerade Zahl. Jede Quadratzahl lässt sich somit aus einer Summe von ungeraden Zahlen darstellen. Es ist sogar so, dass die Summe der ersten n ungeraden Zahlen genau die n-te Quadratzahl n² ergibt.
Beispiel:
Die zehnte Quadratzahl ist gleich der Summe der ersten zehn ungeraden Zahlen: 1+3+5+7+9+11+13+15+17+19=10*10=100
Animation: Darstellung als Summe ungerader Zahlen (1² bis 11²) Jede Quadratzahl n² ist das Doppelte der Summe aus den natürlichen Zahlen von 1 bis zum Vorgänger von n, vermehrt um n.
Jede Quadratzahl n² ist das Doppelte der Summe aus den natürlichen Zahlen von 1 bis zum Vorgänger von n, vermehrt um n.
Beispiel für n=9: 2*(1+2+3+4+5+6+7+8)+9=2*36+9=81
(Die Summe aus den ersten 9 natürlichen Zahlen bezeichnet man als neunte Dreieckszahl D9. Warum diese Zahlen Dreieckszahlen heißen, erfährst du in der Lernumgebung Dreieckszahlen).
Animation: Darstellung als doppelte Summe der ersten n-1 natürlichen Zahlen vermehrt um n (1² bis 11²) Aus der Eigenschaft 2. folgt unmittelbar, dass sich jede Quadratzahl auch als Summe mit zwei aufeinander folgenden Dreiecks�zahlen darstellen lässt. Genauer: die n-te Quadratzahl ist gleich der Summe aus der (n-1)-sten und der n-ten Dreieckszahl.
Aus der Eigenschaft 2. folgt unmittelbar, dass sich jede Quadratzahl auch als Summe mit zwei aufeinander folgenden Dreiecks�zahlen darstellen lässt. Genauer: die n-te Quadratzahl ist gleich der Summe aus der (n-1)-sten und der n-ten Dreieckszahl.
(Die n-te Dreieckszahl berechnet man mit dem halben Produkt aus n und n+1. Siehe Lernumgebung Dreieckszahlen).
Beispiel für n=6: 0,5*5*6+0,5*6*7=0,5*6*(5+7)=36
Animation: Darstellung als Summe der (n-1)-sten und der n-ten Dreieckszahl (1² bis 11²)- Die Teilermenge einer Zahl n besteht aus allen Zahlen, durch die man die „Ausgangszahl“ ohne Rest teilen kann. Genau bei den Quadratzahlen hat diese Teilermenge eine ungerade Anzahl an Elementen.
Beispiel: Die Quadratzahl 36 besitzt die Teiler 1, 2, 3, 4, 6, 9, 12, 18 und 36 - also insgesamt 9 Teiler.
Externer Link zu einem Online-Rechner zur Bestimmung der Teilermenge. - Bildet man bei einer Quadratzahl größer 1 die Primfaktorzerlegung, so tauchen darin gleiche Primfaktoren nur in geraden Anzahlen auf. (In der Potenzschreibweise sind die Hochzahlen der Primfaktoren stets gerade).
Beispiel: 25=5*5=52; 36=2*2*3*3=22*32; 144=2*2*2*2*3*3=24*32
Rechentrick: Quadrate von Zahlen, die auf fünf enden.

Der hier vorgestellte Rechentrick ist leicht verständlich und kann für einfache 5er-Zahlen bereits von Grundschülern durchgeführt werden.
Das nachfolgende Lernvideo 1 beschreibt an mehreren Beispielen ausführlich den Rechentrick und endet mit einem Merksatz.
Dieser Merksatz wird im Lernvideo 2 allgemeingültig bewiesen. Dies ist ein Beispiel für den Einsatz der ersten binomischen Formel. Für die Erklärung werden Grundkenntnisse bei Termumformungen (insbesondere beim Ausklammern) gefordert.
Lernvideo 1: "Einführung der Kopfrechenregel für 5er-Quadrate"
Lernvideo 2: "Beweis der Kopfrechenregel für 5er-Quadrate"
(Vereinfachte) Zusammenfassung der Inhalte aus den Lernvideos:
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Rechentrick: "Quadratzahlen über 25² in zwei Schritten"
Die Quadratzahlen ab 26² lassen sich mit dem nachfolgend vorgestellten Rechentrick elegant in zwei Schritten berechnen.
Kennt man die ersten 15 Quadratzahlen auswendig, wird die Quadratzahlbestimung zu den Zahlen zwischen 35² und 65² besonders einfach. Für die Quadratberechnung zwischen den Zahlen 25² und 35² sowie ab 65² muss man weitere Quadratzahlen auswendig kennen. Kennt man diese nicht, muss man sie mit Hilfe einer Nebenrechnung bestimmen. In solch einem Fall ergeben sich mit dem vorgestellte Trick kaum Rechenvorteile.
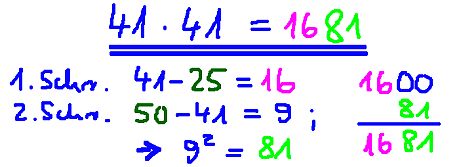
Die Gültigkeit des Rechentricks wird im nachfolgend zum Download angebotenen Dokument bewiesen. Zum Verständnis müssen hierfür die binomischen Formeln bekannt sein.
Schritt 1:
Berechne den Abstand zu 25. Schreibe diesen Wert vor die Zehnerstelle des Ergebnisses.
Schritt 2:
Berechne den Abstand zu 50 und quadriere ihn. Dieser Wert liefert die Einer- und Zehnerstelle des Ergebnisses. Eventuell musst du die Hunderterstelle anpassen. Die ist der Fall, wenn bei Schritt 2 der 50-ziger-Abstand größer gleich 10 ist (- dann liefert das zugehörige Quadrat ebenfalls einen Hundertanteil).
Zusammenfassung (mit Beweis) zum Download
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Mögliche Fragestellungen zum Arbeitsblatt:
- Im Beweis wird der Abstand zur 50 mit der Differenz aus 50 und der Zahl a ermittelt. Wenn a größer als 50 ist, ist es die Differenz aus a und 50 (siehe Beispiele 4 und 5). Warum benötigt man im Beweis keine Fallunterscheidung?
- Der Trick mit den Zahlen 25 und 50 funktioniert, weil -25 * 100 und 50^2 sich aufheben. Bei den Zahlen 4 und 20 ist das auch der Fall (-4 * 100 und 20^2 heben sich auf).
Überprüfe, ob sich die Regel auf diese Zahlen übertragen lässt.
Rechentrick: "Nachbar-Produkte" von Quadratzahlen
Bekanntlich lassen sich Quadratzahlen als Produkt zweier gleicher Zahlen darstellen. Als "Nachbar-Produkt" bezeichnen wir jenes Produkt, dass entsteht, wenn wir einen Faktor um 1 erhöhen und den anderen dafür um 1 vermindern.
Beispiel: Das Nachbar-Produkt zur Quadratzahl 100 wird durch die die Rechnung 9*11 beschrieben. Das nächste Nachbar-Produkt wäre entsprechend 8*12.
Forschungsaufträge:
- Erstelle eine Liste von jeweils neun Nachbar-Produkten zu den Quadratzahlen von 10 bis 15. Suche nach Gemeinsamkeiten. Was fällt auf?
- Suche nach einem Beweis (mit Variablen), mit dem die Güligkeit deiner Vermutung begründet wird.
Arbeitsblatt zum Forschungsauftrag
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Landeswettbewerb Mathematik 2015/16, Runde 1, Aufgabe 3
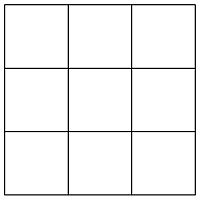
Julia schreibt in jedes Feld des nebenstehenden Quadrates eine der Zahlen von 1 bis 9. Dabei verwendet sie jede Zahl nur einmal.
Nun multipliziert Julia jeweils die drei Zahlen, die in einer Zeile bzw. einer Spalte stehen, und zählt, wie viele der sechs Produkte Quadratzahlen sind.
Finde alle Möglichkeiten für die Anzahl dieser Quadratzahlen.
Hinweise zur Herangehensweise bei der Lösungsfindung:
- „Gefühl für die Lösung mit Zahlenbeispielen“
Setze die Zahlen von 1 bis 9 in verschiedenen Reihenfolgen in das Quadrat ein und berechne die Produkte in den Zeilen und den Spalten.
- „Zusammenhänge finden“
Wann sind die Produkte Quadratzahlen? Findest du eine Vermutung für eine Regel?
Vielleicht hilft es dir, wenn du in Büchern oder im Internet nach „Eigenschaften von Quadratzahlen“ suchst. - „Regel bestätigen oder widerlegen“
Bilde weitere Zahlenbeispiele und bestätige deine Vermutung. Falls sie nicht richtig ist, suche nach anderen Ideen.
- „Ausformulieren der Lösung“
Schreibe deine Überlegungen in eigenen Worten auf, so dass jemand Fremdes sie nachvollziehen kann, der nur die Aufgabenstellung kennt.
- „Kontrolle auf Vollständigkeit“
Hast du nichts vergessen?
Beachte, dass man hier alle Lösungen finden muss. Diese Aufgabenstellung beinhaltet, dass man nachweisen muss, dass keine weiteren Lösungen existieren können. (Die Notwendigkeit dieses Nachweises wird leider oft nicht erkannt).
Vielleicht konntest du durch theoretische Überlegungen zeigen, dass höchstens eine gewisse Anzahl an Lösungen existieren kann. In diesem Fall bist du ebenfalls noch nicht fertig. Finde nun Zahlenbeispiele zu jeder einzelnen Lösung.
Aufgabenstellung mit Hinweisen zum Download:
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Knobelaufgabe: Ein Frosch im Seerosen-Gitter
Die nachfolgende kombinatorische Fragestellung kann von motivierten Kindern bereits in der fünften oder sechsten Klasse gelöst werden. Voraussetzung ist, dass sie bereits Quadratzahlen und Dreieckszahlen kennengelernt haben und wissen, wie man diese durch Summen oder mit der entsprechenden Formel bestimmen kann.
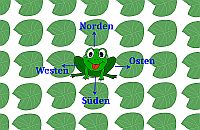
Fragestellung:
Ein (mathematischer) See ist mit unendlich vielen Seerosen bewachsen. Die Blätter der Seerosen sind wie die Gitterpunkte eines rechtwinkligen Koordinatensystems angeordnet.
Ein Frosch sitzt in der Seemitte auf einem Blatt. Er hüpft von Seerosenblatt zu Seerosenblatt, indem er in waagerechter oder senkrechter Richtung auf das jeweilige Nachbarblatt springt - niemals aber in diagonaler Richtung.
An wie vielen verschiedenen Stellen kann er nach 100 Sprüngen sein, wenn er ...
- nur nach oben (= Norden) und nach rechts (= Osten) springen kann.
- in alle Himmelsrichtungen springen könnte, sich dann aber für zwei Richtungen entscheidet. Also entweder nur (wie bei i.) nach Norden/Osten oder nur nach Norden/Westen, nur nach Süden/Osten oder ausschließlich nach Süden/Westen.
- in alle Himmelsrichtungen springt und beliebig oft die Richtung wechselt.
Anspruchsvolle Zusatzfrage:
Auf wie viele verschiedene Arten kann der Frosch in den Fällen i. bis iii. an die Zielpunkte gelangen?
Das nachfolgende Arbeitsblatt beinhaltet Tipps zur Vorgehensweise bei der Suche nach einer Lösung:
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download
Lösungsvorschlag:
Zum Verständnis des Lösungsvorschlags ist etwas Grundwissen zum Thema Dreieckszahlen und Quadratzahlen erforderlich.
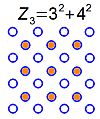
Im Verlauf der Lösung stößt man als Zwischenergebnis auf die Summe von zwei aufeinander folgenden Quadratzahlen. Diese Summen lassen sich (wie Dreieckszahlen oder Quadratzahlen) figürlich darstellen und zählen daher ebenfalls zu den so genannten figurierten Zahlen. Mathematiker bezeichnen sie auch als zentrierte Quadratzahlen.
Bei der Darstellung der Lösung wird im zweiten Teil bei der Berechnung der Anzahl der möglichen Wege die Potenzschreibweise verwendet.
Dokument als OpenOffice-Datei Download ![]()
Dokument als PDF Download







