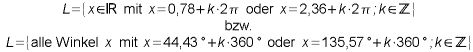Musteraufgabe Sinusgleichung

Diese Aufgabe soll den Nutzen der Einheitskreisskizze bei der Lösung von trigonometischen Gleichungen verdeutlichen.

Wiederholung:

Der Sinus ist über die y-Koordinate eines Punktes P auf dem Einheitskreis definiert. Durch die Lage von P (auf der Kreislinie) ist innerhalb des Intervalls [0°, 360°) bzw. [0, 2*pi) eindeutig ein Winkel im Grad- oder Bogenmaß festgelegt.

Wird umgekehrt ein Sinuswert vorgegeben, ist die Zuordnung zu einem Winkel nicht eindeutig. In der Regel gibt es zwei Winkel, bei denen der zugehörige Punkt auf der Kreislinie diesen Wert als y-Koordinate besitzt. Diese Tatsache soll die folgende Musteraufgabe verdeutlichen.

Musteraufgabe:

Bestimme alle Winkel innerhalb des Intervalls [0°, 360°) bzw. [0, 2*pi), die die folgende Gleichung lösen:

Musteraufgabe zum Sinus

Lösung:

Zunächst formen wir die Gleichung so um, dass wir die linke Seite mit den y-Koordinaten der Punkte auf dem Einheitskreis veranschaulichen können:

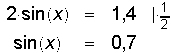
Lösung der Musteraufgabe zum Sinus

Auch die rechte Seite der Gleichung können wir in einem Schaubild interpretieren: Sie stellt eine zur x-Achse parallele Gerade durch den Punkt (0/0,7) dar.

Der Taschenrechner liefert als Lösung den Wert x=0,78 (im Bogenmaß) bzw. 44,43° (im Gradmaß).

In der nachfolgenden Skizze erkennen wir, dass dies nur die halbe Wahrheit ist:

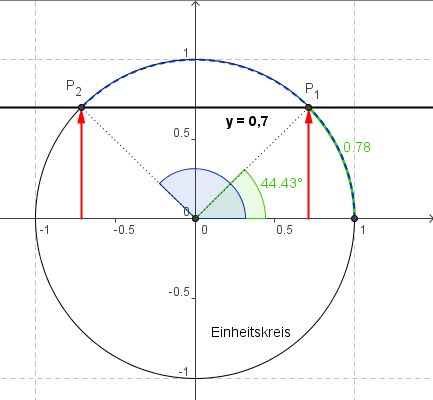
Einheitskreis-Skizze zum Sinus

Aufgrund der Symmetrie folgt die zweite (blaue) Lösung direkt aus der ersten (grünen) Lösung, indem man vom gestreckten Winkel die erste Lösung abzieht: pi-0,78=2,36 (Bogenmaß) bzw. 180°-44,43°=135,57°


Damit haben wir die Aufgabe gelöst: Lösungsmenge

Bemerkungen:

  • Wie sieht die Lösung aus, wenn der erste Winkel größer als pi (bzw. größer als 180°) ist? Wiederhole die Rechnung mit -1,4 (anstatt 1,4) auf der rechten Seite der Gleichung. Welchen Winkel zeigt nun der Taschenrechner an? Wie ist dieses Ergebnis zu interpretieren? (Vergleiche hierzu die Musteraufgabe zum Tangens.) Achte darauf, dass die Lösungen auf das Intervall [0°, 360°) bzw. [0, 2*pi) beschränkt sind.
  • Sollte die Beschränkung auf das obige Intervall nicht gegeben sein, folgen aus jeder der obigen Lösungen unendlich viele weitere indem man ganzzahlige Vielfache von 2*pi oder 360° addiert.
    Die Angabe der Lösungsmenge könnte dann wie folgt aussehen:
  • Lösungsmenge allgemein