Musteraufgabe Kosinusgleichung
Beim Kosinus unterscheidet sich die Einheitskreisskizze etwas von der des Sinus. Wieder muss man die Definition des Kosinus über die Koordinaten des Punktes auf der Kreislinie genau kennen. Die Symmetrie der Skizze liefert anschließend die verschiedenen Lösungen.
Für das allgemeine, mathematische Verständnis lohnt es sich, beide Lösungsvorschläge der folgenden Aufgabe zu behandeln:
Musteraufgabe:
Bestimme alle Winkel innerhalb des Intervalls [0°, 360°) bzw. [0, 2*pi), die die folgende Gleichung lösen:
Lösungsvorschlag 1:
Grundsätzlich sollte man nie durch x oder eine von x abhängige Funktion teilen. Subtrahiere daher auf beiden Seiten der Gleichung cos(x). Wir erhalten damit ein Nullprodukt (Typ: Faktor * Faktor = 0).
Nun müssen wir untersuchen,
für welche x-Werte die beiden Faktoren null werden.
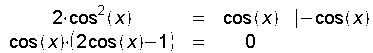
Der erste Faktor ist null, wenn cos(x) gleich null ist. Dies ist für x1=1/2*pi und x2=3/2*pi bzw. α1=90° und α2=270° der Fall.
Auch der zweite Faktor kann null sein. Dies führt zu folgender Gleichung:
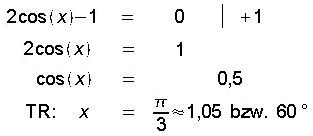
Die Gleichung
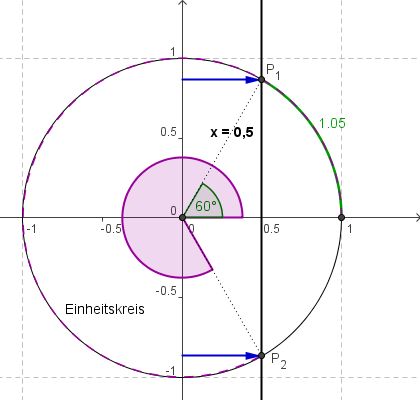
Der Einheitskreis schneidet die Gerade x=0,5 in den Punkten P1 und P2. Der erste Punkt liefert die (obige Taschenrechner-) Lösung pi/3 (oder 1/3*pi). P2 liegt symmetrisch zu P1 bezüglich der x-Achse. Aus der Symmetrie erkennen wir, dass wir die Lösung 1/3*pi vom Vollwinkel abziehen müssen. Somit liefert uns der zweite Faktor unseres Nullprodukts die Lösungen 3 und 4:
-> x3=1/3*pi und x4=2pi-1/3*pi=5/3*pi (bzw. die passenden Lösungen im Winkelmaß α3=60° und x4=360°-60°=300°). Die Lösungsmenge lautet:
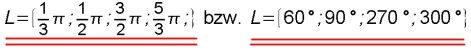
Lösungsvorschlag 2:
Bei dieser Lösungsvariante teilen wir durch cos(x), obwohl wir dies eigentlich nicht tun sollten (vgl. Bemerkung oben). Warum man dies vermeiden sollte, wird weiter unten erklärt. Die erste Umformung ist aus diesem Grund mit einem Stern markiert.
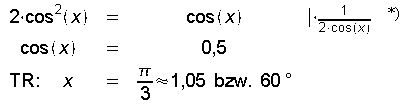
Mit den gleichen Symmetrieüberlegungen wie beim Lösungsvorschlag 1 gelangen wir zur zweiten Lösung:

Unsere Gleichung liefert anstatt vier nur noch zwei Lösungen: 1/3* pi und 5/3*pi bzw. 60° und 300°.
Zwei Lösungen unseres ersten Lösungsvorschlags sind "verloren gegangen". Der Grund hierfür ist die oben erwähnte Fehlerquelle:
*)
Bei unseren Gleichungsumformungen haben
wir bei dem Stern mit einem Ausdruck multipliziert, dessen Nenner für manche Werte von
x null ergibt. Wir wissen bereits seit der Grundschule, dass man durch null nicht teilen darf (und seit der sechsten Klasse, dass ein Nenner niemals null sein darf). Daher müssen wir den Fall cos(x)=0
gesondert untersuchen:
Man sieht der Gleichung ![]() sofort an, dass sie für cos(x)=0 erfüllt ist. Das ist bei x3=1/2*pi und x3=3/2*pi bzw. α3=90° und α4=270° der Fall.
sofort an, dass sie für cos(x)=0 erfüllt ist. Das ist bei x3=1/2*pi und x3=3/2*pi bzw. α3=90° und α4=270° der Fall.
Die Lösungen stimmen mit dem Lösungsvorschlag 1 überein. Wieder ist die Lösungsmenge:
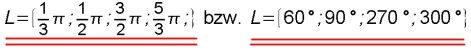
Bemerkungen:
- In einer dritten Lösungsvariante könnte man cos (x) substituieren. In diesem Fall erhielte man eine quadratische Gleichung, die sich durch Ausklammern wiederum in die Form Faktor * Faktor = 0 überführen ließe. Der Unterschied zum ersten Lösungsvorschlag wäre minimal.
- Man möge sich in Zusammenhang mit dieser Aufgabe die "1/3 - 1/2 - Regel" verdeutlichen. 1/3-1/2-Regel


