Aufgabe zur Definitionserweiterung von Sinus und Kosinus

Mit dieser Aufgabe lassen sich Sinus und Kosinus am Einheitskreis dynamisch veranschaulichen. Gleichzeitig wird dabei die neue Definition für die trigonometrischen Zusammenhänge verinnerlicht.

Hinweise:

  • Die Aufgaben können mit Hilfe der nachfolgenden Animation online bearbeitet werden. Zur Anzeige der Animation benötigen Sie Java 1.4 (oder höher). Der erste Aufruf kann etwas dauern.
  • Alternativ kann die Datei einkreis1.ggb heruntergeladen und mit dem (kostenlosen) Programm GeoGebra geöffnet werden. Auch die Aufgabenstellungen können als Datei herunterladen und bei Bedarf abgeändert werden. Den Link zum Download findest du unterhalb der Animation.

Aufgaben:

  1. Projeziere den Punkt P auf die x-Achse. Gib hierzu (unten in der Eingabezeile) P_x=(x(P),0) ein.
    Screenshot
  2. Markiere den Kooridinatenursprung durch Eingabe von (0,0) in die Eingabezeile.
  3. Wähle das Werkzeug "Vektor zwischen zwei Punkten" und konstruiere damit die Verbindungspfeile zwischen Px und P sowie zwischen (0,0) und Px.
    Screenshot
  4. Mit einem Rechtsklick auf den vertikalen Pfeil kannst du seine Eigenschaften verändern.
    Wähle im Reiter "Grundeinstellungen": Beschriftung: sin α und Beschriftung anzeigen: Beschriftung", beim Reiter "Farbe" rot sowie im Reiter "Darstellung" die Linienbreite 7.
    Screenshot
    Die horizontale Pfeil soll blau werden und mit cos α beschriftet werden. Alle Anderen Eigenschaften entsprechen den obigen.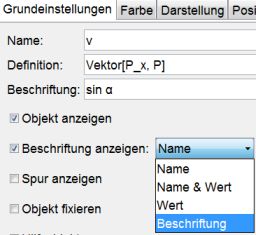
  5. Natürlich kannst du die Projektion von P auf der y-Achse durch Eingabe von P_y=(0,y(P)) erzeugen und Sinus und Kosinus mit den entsprechenden Farbpfeilen veranschaulichen.

Frage:

  • Warum entspricht die Definitionserweiterung für Sinus und Kosinus für Winkel zwischen 0° und 90° exakt der (alten) Definition am rechtwinkligen Dreieck?
    (Erkläre anhand der farbigen Pfeile deiner Animation.)

Aufgaben als OpenOffice-Datei Download
Aufgaben als PDF-Datei Download